La numérisation 3D peut se définir comme l’activité consistant à créer une copie dématérialisée d’un objet ou d’un espace physique existant. Cette définition explique l’emploi récurrent de l’expression “scanner” 3D. Le terme de “scanner” désigne les appareils électroniques permettant de transférer des documents matériels vers des fichiers numériques.
Parvenir à numériser des espaces entiers est une prouesse technologique remarquable et fascinante ! Nous avons désormais la possibilité de créer un double numérique de n’importe quelle chose ayant une existence physique. La science est à l’origine de ces progrès et nous nous devons de saluer le travail fourni par les générations successives de chercheurs et ingénieurs ayant créé le LiDAR, les algorithmes de photogrammétrie numérique ou même les drones.
Dans un monde gouverné par les lois économiques, cette contemplation ne suffira toutefois pas à répondre aux enjeux des marchés.
[qodef_blockquote text= »Numériser oui, mais pourquoi faire ? » title_tag= »p » width= » »]Il est temps de redescendre vers un niveau plus opérationnel en étudiant les utilisations pouvant être faites des données 3D issues de la numérisation.

Qualification des données 3D
Au terme des missions de captation, qu’elles soient photogrammétriques ou LiDAR, une des premières étapes est de “qualifier” les données 3D afin d’améliorer leur valeur et leur employabilité. Ce premier niveau de valorisation peut prendre la forme d’activités très disparates et cumulables.
Évidemment, le type de qualification des données dépend des applications attendues, définies par les enjeux stratégiques régissant le marché ayant justifié le lancement d’une mission de numérisation.
[qodef_blockquote text= »Qualifier les données 3D a donc pour objectif de leur attribuer la plus grande valeur possible et devient à ce titre une étape à forte valeur ajoutée. » title_tag= »p » width= » »]C’est justement sur cette étape du processus que les écarts qualitatifs les plus importants sont constatés entre les entreprises expérimentées et les amateurs.
Calage dans un système de coordonnées
La Terre n’est pas plate
J’espère que cette information ne va pas vous surprendre !

Le but n’est pas d’enfoncer des portes ouvertes mais d’introduire la notion de “système de coordonnées”, désignant un référentiel dans lequel nous pourrons représenter des éléments dans l’espace.
Appliqué à la cartographie et au géopositionnement, un système de coordonnées permet de définir la position sur le globe de n’importe quel point en se basant sur ses coordonnées.
Si la Terre était plate, la définition des coordonnées d’un point pourrait être très simple : nous pourrions par exemple considérer que l’origine du système serait un point de coordonnées X, Y et Z nulles situées “au coin inférieur gauche de la carte”. Le gros avantage serait de pouvoir connaître les distances entre chaque point très facilement en se basant sur leurs coordonnées. Une simple soustraction suffirait à déduire qu’un point de coordonnées x=100, y=500 et z= 50 est distant de 50 mètres d’un point de coordonnées x=150, y=500 et z=50.
Grâce à la trigonométrie, ces calculs restent très simple même lorsque les points ne sont pas sur le même axe. Ainsi, la distance entre les points de coordonnées (100,500,50) et (150,550,50) sera égale à la racine carrée de la somme des distances sur les axes X et Y au carré :
Distance = √ [ (150 - 100)² + (550 - 200)² ]Distance = √ [2500 + 2500] = 70,71 mètres
Quiconque a déjà entendu parler du théorème de Pythagore comprendra aisément la méthode de calcul employée ici.
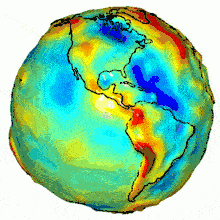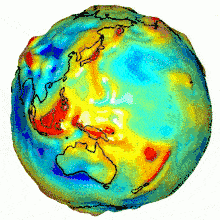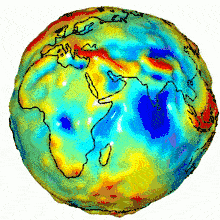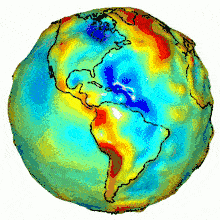
[qodef_blockquote text= »Si seulement la Terre était plate, la géographie serait donc très simple. Mais la Terre est ronde… enfin non, même pas, elle est plutôt ovoïde… ou presque. » title_tag= »p » width= » »]Au delà de la forme physique de la Terre, une autre composante entre en jeu dans le calcul des coordonnées, notamment pour l’altitude : la pesanteur. Or cette dernière n’est pas constante en tous points. Afin de permettre des mesures précises d’altitude, il a fallu inventer le terme de “géoïde” pour modéliser le champ gravitationnel de la surface terrestre.
L’importance des systèmes de coordonnées
D’apparence si sphériquement parfaite depuis l’espace, notre planète masque en fait les nombreuses petites irrégularités de sa surface. Bien que ces imperfections lui donnent du charme, les cartographes n’y sont pas sensibles. Ce qu’ils veulent, c’est modéliser cette surface de manière exploitable. Ils utilisent donc une figure géométrique plus régulière, l’ellipsoïde. Ce volume globalement sphérique présente un aplatissement aux pôles et sert de référence pour la construction des projections cartographiques.
[qodef_blockquote text= »Les cartes existaient bien avant les satellites. L’Humain savait déjà que ses pieds ne reposaient pas sur une surface plane, mais il n’avait pas pour autant la capacité de définir précisément la géométrie de la planète. » title_tag= »p » width= » »]Définir un système de coordonnées mondial n’étant pas envisageable, une multitude de systèmes de coordonnées locaux ont vu le jour, chacun ayant une zone de validité limitée. En effet, tout système de projection déforme les surfaces et distances, il est donc utile de pouvoir choisir le meilleur système de projection en fonction de sa position sur le globe. Ainsi, rien qu’en France métropolitaine, il existe plus d’une dizaine de systèmes coordonnées différents.

La possibilité de définir des systèmes globaux pour l’ensemble de la Terre est apparue avec les satellites notamment avec la mise en œuvre du système GPS et autres GNSS. Ceux-ci expriment les coordonnées dans le système géocentrique WGS 84 (World Geodetic System 1984). Ce système géodésique mondial est composé d’un système de coordonnées, d’un ellipsoïde de référence (l’ellipsoïde de révolution IAG GRS 80) et d’un géoïde (EGM96).
[qodef_blockquote text= »Les coordonnées ne sont plus exprimées par des distances sur des axes cartésiens, mais par des angles exprimés en degrés géographiques. » title_tag= »p » width= » »]
Numérisation 3D et géopositionnement
Le sujet qui nous unit étant de capturer la réalité physique d’un site, tenir compte de la position exacte sur le globe de cette même scène sera souvent indispensable.
En effet, l’intérêt majeur de la numérisation 3D réside dans sa capacité à conserver une double numérique d’une scène à un instant T. De ce fait, les applications en termes de suivi et de contrôle des évolutions d’une scène sont nombreuses : suivi des glissements de terrain, des déformations d’ouvrages, de la progression des travaux…
[qodef_blockquote text= »Toutes ces applications consistent à ajouter une dimension temporelle aux trois dimensions spatiales. On parle communément de 4D : trois dimensions plus le temps. » title_tag= »p » width= » »]Pour comparer deux scènes à des instants différents, il est évidemment nécessaire que les données 3D puissent se superposer.
Inscrire les données 3D dans un système de coordonnées devient donc indispensable dès lors qu’un suivi devra être réalisé. Mais ce n’est pas la seule raison.
Redressement des données
Les données 3D doivent également être redressées afin de correspondre à une réalité physique.
[qodef_blockquote text= »Personne ne souhaite que le nuage de points de son bâtiment soit incliné comme la Tour de Pise… Sauf s’il scanne la Tour de Pise 😉 » title_tag= »p » width= » »]Une telle aberration nous sauterait aux yeux instantanément, mais un ordinateur ne la remarquera pas. Il est nécessaire de définir la bonne inclinaison d’un modèle 3D sur chacun des axes.

Avant toute mission de numérisation par scanner laser 3D ou photogrammétrie, il est indispensable de positionner un minimum de trois cibles pour lesquelles un géomètre a précisé les coordonnées. En effet, trois points suffisent à définir un plan dans l’espace et ainsi à redresser le modèle. Toutefois, dans la pratique, il sera préférable d’augmenter le nombre de cibles afin de diviser les écarts et de compenser une éventuelle erreur dans les coordonnées ou un déplacement des cibles.
Dans le cas des modèles photogrammétriques, gardez également à l’esprit que ce redressement ne constitue qu’une partie du travail. Rappelons qu’un modèle photogrammétrique est obtenu par corrélation d’images sur la base de simples photographies. Un modèle photogrammétrique ne se base donc pas sur une mesure des distances in-situ. Le modèle n’est donc pas du tout à l’échelle.
Mesurer des distances sur le mesh ou le nuage de points brut renverra des résultats très loins de la réalité physique. Mais le ratio sera constant d’une mesure à l’autre : le modèle 3D est cohérent mais il doit être mis à l’échelle et être redressé.

En ajoutant des points de calage à un modèle photogrammétrique, on ajoute les informations nécessaires au redressement des données ainsi qu’à la réalisation d’une homothétie (mise à l’échelle) de celles-ci.
Validation de l’assemblage des scans
Lors d’une numérisation par scanner laser 3D en station fixe, chaque position de scan génère un nuage de points “perdu dans l’espace”. Chaque point est défini par une distance, un angle vertical et un angle horizontal exprimés sur la base de l’origine du scanner. Le nuage de points “global” de la scène n’est obtenu qu’après assemblage de ces nuages de points isolés.
Ce travail d’assemblage est réalisé de manière plus ou moins automatique en fonction du matériel et des logiciels retenus, mais repose dans tous les cas sur la même méthode dite de “cloud-to-cloud” (nuage à nuage) permettant de trouver l’assemblage le plus pertinent de deux nuages de points isolés.
Les indicateurs de qualité
La qualité de cet assemblage est évaluée sur plusieurs critères. Le premier indicateur est le taux de recouvrement. Il s’agit de la proportion de points communs entre les deux nuages. Un recouvrement important est facile à obtenir : il suffit de multiplier les stations de scan. C’est grâce à ce recouvrement que les logiciels d’assemblage de scan peuvent travailler de manière automatique.
Un second indicateur généralement évalué par les logiciels de traitement des scans est le risque de glissement. Il s’agit de la répartition des points communs sur différents plans permettant de stabiliser la scène. Un moyen d’illustrer ceci est d’imaginer la numérisation scanner laser 3D d’une autoroute. Dans le sens transversal, le risque de glissement des données 3D est très faible : les glissières constituent des points caractéristiques évidents. En revanche, dans le sens longitudinal, le glissement sera souvent très important : aucun élément caractéristique ne différencie l’autoroute dans le sens de la longueur, si ce n’est parfois l’environnement, selon sa nature.
Dans de telles circonstances, il sera recommandé d’employer des cibles et sphères pour réduire le risque de glissement.
Le dernier indicateur pouvant aider à l’évaluation de la qualité de l’assemblage est nommé “erreur RMS”. Ce terme vient de l’anglais “Root Main Square”, méthode statistique permettant d’évaluer la variance d’une série de données, désignant en quelque sorte l’erreur moyenne d’un groupe de données au regard de la distribution globale de ces dernières. Il s’agit, de manière très simplifiée, d’une évaluation de l’écart-type des nuages de points isolés au regard de l’assemblage global proposé par le logiciel.
[qodef_blockquote text= »Une erreur RMS élevée devra immédiatement alerter la personne chargée de l’assemblage des scans. » title_tag= »p » width= » »]
Evaluation humaine de la qualité de l’assemblage
Les méthodes statistiques ne peuvent suffir à valider un assemblage de scans 3D. En cas de recouvrement assez faible ou d’une scène ayant subit de nombreuses modifications en cours de numérisation, telle que la numérisation d’une rue piétonne, les données servant à l’évaluation peuvent générer de mauvaises interprétations algorithmiques.
[qodef_blockquote text= »Un regard humain est donc nécessaire pour valider le travail d’assemblage réalisé au travers d’un logiciel. » title_tag= »p » width= » »]Il s’agira ici de procéder à des sondages sur le nuage de points dans le but de détecter d’éventuelles aberrations. Certaines sont assez simples à détecter :
- un faux-aplomb sur un mur,
- une “double peau” : dédoublement d’une surface, mur ou plancher,
- une “pièce fantôme” : souvent causée par des reflets, il s’agit de scans 3D positionnés à des endroits n’ayant jamais existé (en lévitation à l’extérieur d’un bâtiment par exemple).
Décimation ou sous-échantillonnage des données
Les meshs (faces 3D décrivant une surface texturée de la scène, généralement obtenues par photogrammétrie) et nuages de points constituent des données volumineuses. Très volumineuses.
[qodef_blockquote text= »Un scanner laser 3D capte entre 500 000 et 2 millions de points par seconde et la photogrammétrie peut atteindre des résolutions sub-millimétriques. » title_tag= »p » width= » »]Cette masse de données est séduisante dans une quête de précision absolue, mais l’est beaucoup moins lorsqu’il s’agit d’acheter des disques durs capables de la stocker, et des ordinateurs ayant les ressources matérielles suffisantes pour l’exploiter sans latences insupportables.
Il est nécessaire de définir précisément l’objectif de la numérisation 3D pour chaque cas. Si vous souhaitez numériser un bâtiment historique qui menace de disparaître dans le but d’en conserver une double numérique, alors la précision absolue a tout son sens.
En revanche, si vous numérisez un étage de bâtiment dans le but de produire un plan d’évacuation, alors clairement, il ne sera pas utile de s’encombrer de l’ensemble des données captées par la numérisation 3D.
[qodef_blockquote text= »L’idée même de supprimer une partie des données collectées sur le terrain dérange beaucoup. Nous basculons d’un monde où l’arpentage était une activité chronophage, vers un monde d’abondances voire d’excès d’informations spatiales sur notre environnement. » title_tag= »p » width= » »]Ce changement de paradigme engendre de l’inconfort à l’idée de ne pas valoriser certaines données collectées. Il est important de rester rationnel et de ne pas rentrer dans la quête du “toujours plus” lorsque cela n’est pas nécessaire.
Une méthode vise justement à alléger les données de numérisation 3D, par nature volumineuses, afin de les rendre plus légères. Il s’agit du sous-échantillonnage des données, également appelé “décimation”. Il s’agit de définir la suppression de certaines données du nuage de points ou du mesh capturé en 3D. Plusieurs méthodes sont généralement proposées par les logiciels de traitement des données 3D.

Sous-échantillonnage aléatoire
La première méthode est dite “aléatoire”. Le logiciel supprime les données de manière aléatoire afin d’atteindre le nombre final de points ou de faces demandé par l’utilisateur, ou exprimé en proportion de la quantité initiale d’informations. Le terme aléatoire peut être entendu de manière péjorative comme un synonyme du terme “approximatif”. Il est important de rappeler ce qu’est la “loi des grands nombres”.
Un dé comporte six faces. Si vous le lancez, vous avez une chance sur six de tomber sur le chiffre que vous aurez choisi. Pourtant, si vous lancez le dé six fois de suite, vous n’avez pourtant que très peu de chances de voir apparaître successivement chaque face du dé. Il y aura très probablement des chiffres qui ne seront pas sortis. Pourtant, si vous lancez ce même dé 6 millions de fois, chaque face apparaîtra environ 1 million de fois.
S’il est vrai de dire qu’une suppression aléatoire des données conduit à une approximation sur un faible volume de données, ça l’est beaucoup moins lorsque le volume des informations est très conséquent. Or, un nuage de points comporte généralement plusieurs dizaines à plusieurs centaines de millions de points. La méthode aléatoire est ainsi la meilleure méthode pour réduire un nuage de points tout en gardant une répartition de la densité identique à la répartition initiale.
Ainsi, les zones ayant la meilleure résolution spatiale dans le nuage brut seront également celles ayant la meilleure densité de points après sous-échantillonnage.
Sous-échantillonnage par distance entre les points
Cette méthode d’allègement des nuages de points 3D a beaucoup plus de sens dans une application en bâtiment. Pour l’illustrer, imaginez-vous en train de scanner votre bureau. Vous positionnez le scanner 3D dans un angle de la pièce. Lors de la rotation horizontale, le scanner laser 3D va balayer toute la pièce :du mur opposé situé à 4 mètres au mur situé juste à l’arrière du scanner, dans l’angle, à tout juste 10 centimètres.
Or, la sphère de signaux laser qui est envoyée par le scanner laser 3D lors de sa rotation, est répartie de manière homogène sans considération de la distance de l’objet visé. Ainsi, la résolution spatiale du nuage de points sera nettement supérieure sur le mur situé à 10 centimètres que sur celui situé à 4 mètres : le nombre de points par centimètre carré sera supérieur.
Un autre phénomène provient de l’étape d’assemblage des scans. Lorsque chaque nuage de points isolés est assemblé à ses voisins pour former un nuage global, les géométries communes de la scène sont utilisées et les points situés dans ces zones de recouvrement sont intégralement conservés. Les données se superposent, augmentant encore la densité de points.

Ce double phénomène conduit à une inflation du nombre de points mais également à répartition très disparate de leur densité. Certaines zones auront une résolution spatiale (distance entre les points) parfois 10 à 100 fois supérieure à d’autres zones, plus distantes ou ayant fait l’objet de moins de recouvrement entre stations. Pour des applications en bâtiment par exemple, notamment en vue de la modélisation d’une maquette numérique BIM, il sera plus important d’obtenir un nuage de densité homogène que d’obtenir un point tous les centièmes de millimètres dans les angles des pièces.
Définir une règle de sous-échantillonnage basée sur la distance minimale entre chaque point permet justement d’homogénéiser la densité d’informations. Il s’agit ici de demander au logiciel de supprimer tous les points distants de leur voisin le plus proche d’une valeur inférieure à la valeur définie. En clair, si l’on souhaite obtenir une résolution de 3 millimètres, tous les points ayant un voisin plus proche d’eux que cette distance seront éliminés.
Nettoyage des points aberrants et réduction du bruit
Un nuage de points obtenu par lasergrammétrie LiDAR ou un mesh obtenu par photogrammétrie ne constituent pas une donnée directement exploitable. Les conditions météorologiques (pluie, brouillard…), les mouvements de la scène (végétation sous l’effet du vent, véhicules, personnes, matériels en mouvement…) ou la nature des matériaux (reflets, diffraction dans les matières translucides…) génèrent des artefacts. Ces aberrations dans les données 3D ont non seulement pour effet d’alourdir inutilement les fichiers, mais également d’en perturber la compréhension et la visualisation.

Un nettoyage est donc nécessaire. De nombreux algorithmes existent et peuvent être lancés soit de manière locale sur un ordinateur, soit en mode “cloud” sur des serveurs de calcul.
Les algorithmes les plus simples agissent en créant des groupes de points basés sur leur proximité et leur densité. Les plus petits groupes sont alors souvent des artefacts, qu’il convient donc de supprimer. Un regard humain reste nécessaire pour définir le contenu des groupes créés et déterminer s’il est pertinent ou non de les conserver.
Certaines méthodes de filtrage des nuages de points utilisent des procédés statistiques pour déterminer quels points constituent une donnée valide et quels autres ne sont que du “bruit”. Ces techniques partent du postulat que les données valides constituent des ensembles de données plus denses que les autres.
Les algorithmes tels que le Statistical Outlier Removal (SOR) de la bibliothèque PCL calculent la distance moyenne de chaque point par rapport à ses voisins puis rejette les points plus éloignés de la distance moyenne. Il s’agit en quelque sorte des mêmes méthodes que celles employées par les statisticiens pour éliminer certaines valeurs d’un groupe afin de ne garder qu’un échantillon de données dit “représentatif”.
La donnée 3D peut également détenir une information pouvant contribuer à sa classification et si nécessaire à sa suppression. Les nuages de points produits à l’aide de scanners laser (LiDAR) multi-écho permettent ainsi de filtrer de manière automatique de grands jeux de données avec une plus grande pertinence que les méthodes statistiques et avec plus de précision qu’un travail manuel.

Ainsi, la végétation pourra aisément être filtrée au cas où nous ne souhaitions conserver que le nuage de points représentant le sol : il suffira de ne conserver que le dernier écho. De la même manière, en cas de numérisation extérieure par temps de pluie, le premier écho à de fortes chances de correspondre aux gouttes ayant été impactées par le laser.
Les LiDAR multi-spectraux et hyper-spectraux permettent également de caractériser les données. En effet, selon le profil spectral du signal retour (réflectance du signal sur différentes bandes de fréquences), la nature du matériau impacté peut être déterminée. Ces applications sont pour l’heure réservées à des numérisations à très grande échelle (satellites météo, LiDAR aéroportés sous avions…).
Caractérisation des nuages de points par intelligence artificielle
La méthode la plus avancée technologiquement consiste à employer l’Intelligence Artificielle pour procéder au nettoyage et à la caractérisation des nuages de points. Le constat est clair : les méthodes mathématiques et statistiques ne sont pas suffisamment adaptables pour permettre de comprendre une scène numérisée en 3D. L’humain reste encore aujourd’hui nécessaire, mais pour combien de temps ?
Les géants de la Tech bâtissent d’énormes datacenters et investissent des milliards dans la recherche et développement de solutions informatiques permettant de remplacer le cerveau humain. Nous parlons désormais de “réseaux neuronaux” pour désigner des clusters (groupes) d’ordinateurs ayant pour vocations de distribuer le travail d’analyse d’une information et de paralléliser les hypothèses. Les machines peuvent désormais apprendre de cette façon. On parle alors de “deep learning” (apprentissage profond) pour désigner cette capacité.

Les ordinateurs ne sont plus de simples exécutants, produisant le travail demandé par un humain qui garde alors charge de valorisation d’un résultat. Désormais l’intelligence artificielle se substitue à l’humain dans ce travail de valorisation et de capitalisation des informations.
Chaque analyse est décomposée en hypothèses qui sont traitées par des clusters et dont les résultats sont comparés aux expériences précédentes pour déterminer quelle hypothèse est la plus pertinente. L’humain ne sert plus alors qu’à amorcer la machine en validant les premières hypothèses. Si vous êtes parent, vous remarquerez probablement que ce processus est bel et bien une méthode d’apprentissage en tous points comparable à celle employée par vos enfants pour leurs premiers pas.
Appliquée aux données de numérisation scanner 3D et photogrammétrie, la méthode est la même. Les données d’entrées sont des nuages de points, donnant de précieuses informations sur la géométrie 3D d’une scène, mais également des photos, ayant servi au travail de reconstruction photogrammétrique ou bien ayant été prises par le scanner laser 3D lors de la captation.
Progressivement et sur la base de ces données, les IA (Intelligence Artificielle) détectent que de grandes surfaces planes et horizontales situées sous le trépied du scanner 3D sont des planchers, qu’une ouverture rectangulaire dans une surface plane et verticale est un passage de porte. Puis l’IA devient capable de déterminer que le groupe de points dans le nuage, formant plusieurs plans verticaux décrivant une rotation autour de cette ouverture de porte, est une donnée parasite générée par la porte ayant été bougée par l’opérateur lors de la numérisation.
[qodef_blockquote text= »Les méthodes basées sur les statistiques, les échos multiples ou l’analyse spectrale LiDAR sont très répandues depuis de nombreuses années dans le monde de la cartographie. En revanche, utiliser une intelligence artificielle dans le processus n’est pas encore quelque chose de banal. » title_tag= »p » width= » »]Cette perspective est née de la rencontre presque forcée du “monde de la tech” et de celui de la cartographie autour du développement des véhicules autonomes. Les véhicules autonomes doivent numériser leur environnement pour être capable d’y évoluer. Mais ils doivent également le comprendre en caractérisant les nuages de points captés par le LiDAR. Le but est bien évidemment d’éviter que les véhicules autonomes ne soient responsables d’erreurs d’appréciation sur leur environnement, pouvant avoir des conséquences mortelles.

Compte tenu de l’évolution incroyablement rapide des véhicules autonomes, la convergence technologique permettant une application courante et à grande échelle de la caractérisation automatique des données de numérisation 3D appliquée au bâtiment est très proche.

